Medidas de tendencia central!!! y Media geométrica...

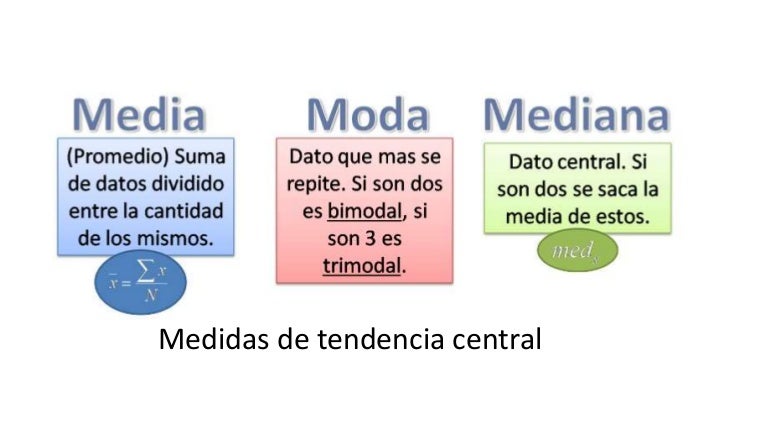
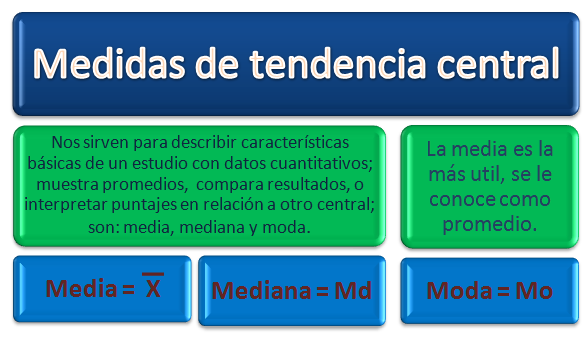
Medidas de Tendencia Central:

Las medidas de tendencia central son medidas estadísticas que pretenden resumir en un solo valor a un conjunto de valores.

Las medidas de tendencia central más utilizadas son: 

MEDIA ARITMÉTICA:
La media aritmética es el valor promedio de las muestras y es independiente de las amplitudes de los intervalos.

MODA:
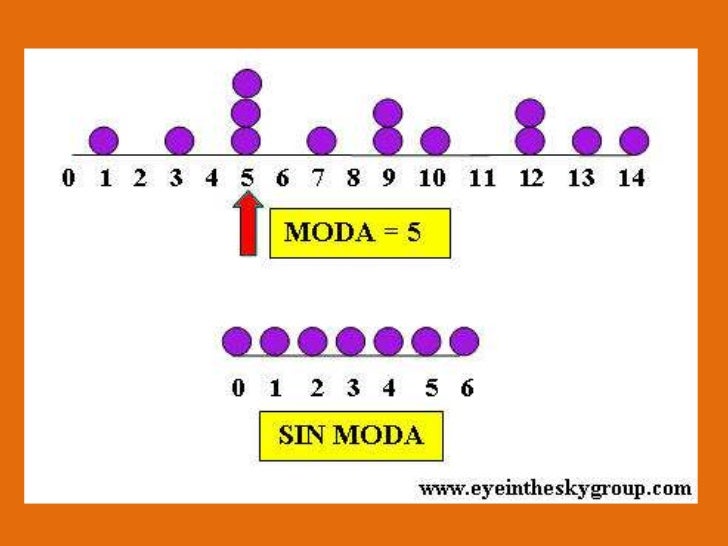
Se trata de un conjunto de prendas de vestir, adornos y complementos que se basan en gustos, usos y costumbres, y que se usan durante un periodo de tiempo determinado.

MEDIANA:
Espacio de separación, zanja o pared baja con que se separan los dos sentidos de la circulación en una autopista o autovía para impedir el paso de los vehículos al carril contrario.

Cuando se hace referencia únicamente a la posición de estos parámetros dentro de la distribución, independientemente de que esté más o menos centrada, se habla de estas medidas como medidas de posición.

MEDIA GEOMÉTRICA:

En matemáticas y estadística, la media geométrica de una cantidad arbitraria de números (por decir n números) es la raíz n-ésima del producto de todos los números, es recomendada para datos de progresión geométrica, para promediar razones, interés compuesto y números índices.

${\displaystyle {\bar {x}}={\sqrt[{n}]{\prod _{i=1}^{n}{x_{i}}}}={\sqrt[{n}]{x_{1}\cdot x_{2}\cdots x_{n}}}}$

Por ejemplo, la media geométrica de 2 y 18 es

${\displaystyle {\sqrt[{2}]{2\cdot 18}}={\sqrt[{2}]{36}}=6}$

Otro ejemplo, la media de 1, 3 y 9 sería

${\displaystyle {\sqrt[{3}]{1\cdot 3\cdot 9}}={\sqrt[{3}]{27}}=3}$

Ventajas

• Considera todos los valores de la distribución
• Es menos sensible que la media aritmética a los valores extremos.

Desventajas

• Es de significado estadístico menos intuitivo que la media aritmética.
• Su cálculo es más difícil.
• Si un valor ${\displaystyle x_{i}=0\,}$ entonces la media geométrica se anula o no queda determinada.

Solo es relevante la media geométrica si todos los números son positivos. Como hemos visto, si uno de ellos es 0, entonces el resultado es 0. Si hubiera un número negativo (o una cantidad impar de ellos) entonces la media geométrica sería o bien negativa, o bien inexistente en los números reales.

En muchas ocasiones se utiliza su trasformación en el manejo estadístico de variables con distribución no normal.

La media geométrica es relevante cuando varias cantidades son multiplicadas para producir un total.

Propiedades[editar]

• El logaritmo de la media geométrica es igual a la media aritmética de los logaritmos de los valores de la variable.
• La media geométrica de un conjunto de números positivos es siempre menor o igual que la media aritmética:

${\displaystyle (x_{1}x_{2}\dots x_{n})^{\frac {1}{n}}\leq {\frac {x_{1}+x_{2}+\dots +x_{n}}{n}}}$

La igualdad sólo se alcanza si ${\displaystyle x_{1}=x_{2}=\dots =x_{n}}$.